Ophiuride
Die Ophiuride (von griechisch ὁ ὄφις ‚die Schlange‘ und ἡ οὐρά ‚der Schwanz‘, deshalb auch Schlangenschwanzlinie genannt) ist eine algebraische Kurve vom Grad 3. Sie ermöglicht das geometrische Lösen der beiden zentralen klassischen Probleme der Antike, der Würfelverdopplung und der Dreiteilung des Winkels. Damit ist sichergestellt, dass alle kubischen Gleichungen mit dieser Kurve zu lösen sind (siehe Abschnitt Lösen kubischer Gleichungen). Dazu erfordert es jeweils nur den Schnitt der Kurve mit einer Geraden.[1]
Historisches
Urheber der Kurve ist der Autodidakt Diedrich Uhlhorn. Als Mathematiker ist er nie hervorgetreten. Im weiteren Leben wurde er allerdings berühmt als Pionier des Maschinenbaus. Der Bau seiner Münzpresse (1817) bahnte dem Kniehebelprinzip den Weg. Im Jahr 1809 brachte dieser Uhlhorn ein Buch heraus mit dem Titel „Entdeckungen in der höhern Geometrie“. Darin stellt er zahlreiche höhere Kurven vor, zusätzlich auch Werkzeuge zu deren Erzeugung. Die Ophiuride gibt den Auftakt. Ihre Bezeichnung leitet er her aus dem Alt-Griechischen: „Schlangenschwanzlinie“.[2] Erklärtes Ziel bei der Vorstellung dieser Kurve ist es, einen Großteil der antiken Lösungen zu den „Großen Problemen“ (Würfelverdopplung, Dreiteilung des Winkels) – die berüchtigten „Neusis-Konstruktionen“ –, zu befreien von dem Vorwurf, eine Umsetzung sei hier nur möglich „mittels Probieren“. J. Chr. Sturm hatte von „Hin- und Wiederrukken“ eines Lineals gesprochen (1670),[3] Montucla erstmals von „Herumfummeln“ (« une sorte de tâtonnement », 1758).[4] Uhlhorn betont wiederholt: „Ohne Probieren lässt sich das Gesuchte auf folgende Art finden: …“[5][6]
Die Kurve, die Uhlhorn vorstellt – sozusagen „zur Rettung der antiken Lösungen“ – zeichnet sich zunächst einmal dadurch aus, dass sie perfekt eingepasst ist in das Umfeld der aus der Antike überlieferten Lösungen: Auch die Lösungen von Nikomedes basieren auf einer Kurve, der Konchoide. Dazu gehört ein Werkzeug zu deren Erzeugung. Dies Paket gilt später als wegweisend. Uhlhorn stellt sogar drei Geräte zur Erzeugung seiner Kurve vor – wie im Folgenden gezeigt –, ausgehend von unterschiedlichen Lösungsansätzen der Antike (Platon, Apollonius und Philo). Er betont „daß sich also eine und dieselbe Linie auf drey verschiedene Arten erzeugen läßt.“ Dem hier abgebildeten Gerät (siehe Abschnitt Mittels Doppelgnomon) gibt er aber den Vorzug, „weil es sehr zuverlässig und sicher ist.“[7]
Der Ansatz der Lösung „Platon“ legt einen Rückgriff auf eine Kurve nahe. Das war bereits Th. Heath aufgefallen. In seiner History of Greek Mathematics (1921) – mehr als 100 Jahre nach Uhlhorn – leitet er die Gleichung einer Ortskurve her. Diese Gleichung stellt die Ophiuride dar. Eine Darstellung der Kurve fehlt hier ebenso wie eine Bezeichnung.[8] Anders bei W. R. Knorr: Dieser mutmaßt, die Bezeichnung sei erst in der Neuzeit aufgekommen und er verweist auf das Buch von Uhlhorn. Zu der Kurve selbst meint Knorr, sie könne auf Eudoxus zurückgehen. In der Kissoide des Diokles erkennt er einen Spezialfall der Ophiuride. Eigentlich habe sogar Platon diese Kurve erfinden können. Das Gerät, das diesem zur Lösung des Delischen Problems zugeschrieben wird, lege jedenfalls einen Einsatz als Kurvenplotter nahe: “the method for doing so is evident.”[9] Das erste der Uhlhornschen Zeichengeräte für die Ophiuride setzt eben diesen Ansatz praktisch um.
Definition
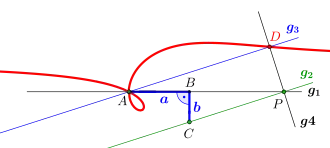
Gegeben sei ein Rechtwinkelhaken mit den Kantenlängen und . Der Punkt bewege sich auf der Kantengeraden . Die Ophiuride zum Rechtwinkelzug ist dann die Ortslinie des Schnittpunktes der Parallelen zu durch mit der Senkrechten zu in .
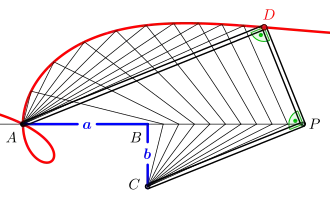
Eine Gleichung der Ophiuride leitet Uhlhorn allgemein her:[10]
- .
- „Bei Uhlhorn sind x und y vertauscht“[10]
Im Eingangsbeispiel führt das auf die Gleichung
- .
Wählt man andererseits so erhält man leicht die Schar
- .
Erzeugung
Als Lotfußpunktkurve einer Parabel
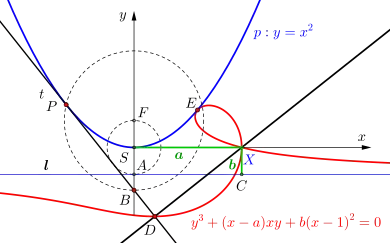
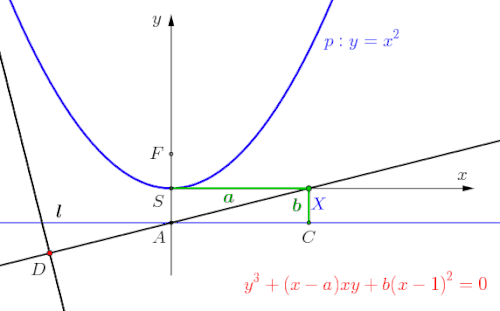
Gegeben sei eine Parabel , die zugehörige Leitlinie. sei ein beweglicher Punkt auf der Parabel , die zugehörige Tangente. sei ein beliebiger Punkt auf einer Linie, die parallel zur Leitlinie und durch den Scheitel verläuft. Die Ortslinie des Schnittpunkts von mit dem Lot von auf ist dann eine Ophiuride. Ist der Scheitelpunkt der Parabel , so ergibt sich die Kissoide des Diokles.[11]
Konstruktion[12]
Es beginnt mit dem Einzeichnen der Parabel mit Scheitelpunkt , dem Ursprung eines kartesischen Koordinatensystems. Der Kreis mit Radius (entspricht des Koeffizienten der Parabelgleichung ) um Punkt schneidet die -Achse im Brennpunkt und im Punkt . Durch wird die Leitlinie parallel zur -Achse gezogen.
Der bewegliche Punkt wird auf die Parabel gesetzt, anschließend die zugehörige Tangente bestimmt. Hierzu dient ein Kreis mit Radius um den Punkt , generiert wird damit der Schnittpunkt auf der -Achse. Nach dem Ziehen der Tangente durch und setzt man den festen Punkt beliebig auf die -Achse. Eine Senkrechte durch schneidet die Leitlinie in . Im dargestellten Beispiel hat der Rechtwinkelhaken die Längen und . Abschließend zieht man eine, auf die Tangente senkrecht stehende Gerade durch . Schnittpunkt ist , der liegt auf der Ortslinie der Ophiuride.
Wird der Punkt auf der Parabel bewegt, (siehe Animation), generiert Punkt den Graphen der Ophiuride mit deren Berührpunkt auf der Parabel:
Als Medianlinie von Kreis und Gerade
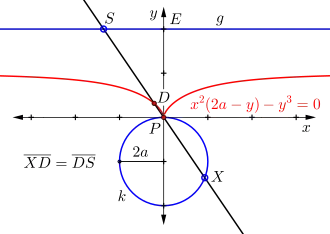
Gegeben sei ein Kreis und eine Gerade außerhalb. sei ein fester Punkt auf dem Kreis . sei ein beliebiger Punkt auf . Die Strecke sei verlängert bis zum Schnittpunkt mit der Geraden . Die Ortslinie der Mittelpunkte der Strecke ist dann eine Ophiuride. Die Kissoide des Diokles ergibt sich hier, wenn der Punkt auf dem Lot vom Zentrum des Kreises auf die Gerade liegt.[14]
Konstruktion[15]
- Für die nebenstehende Darstellung „Ophiuride gleich Kissoide des Diokles ...“ setzt man beispielsweise den Kreis mit Radius auf die Koordinaten eines kartesischen Koordinatensystems. Schnittpunkt ist . Nach dem Bestimmen des Punktes wird die zur -Achse parallele Gerade gezogen. Nun wird der Punkt beliebig auf den Kreis gesetzt. Es folgt eine Gerade, die durch und verläuft und dabei den Schnittpunkt generiert. Abschließend wird die Strecke in halbiert. Der so erzeugte Punkt liegt auf der Ortslinie der Ophiuride.
- Wird der Punkt auf der Geraden bewegt, generiert Punkt den gesuchten Graphen der Ophiuride gleich einer Kissoide des Diokles, darin ist :
- [16]
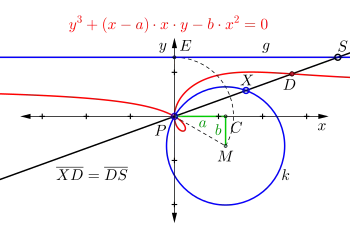
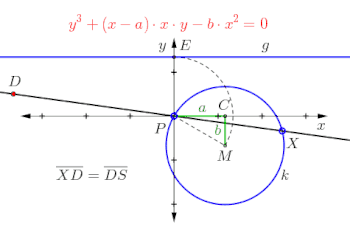
- Für die darunter stehende Darstellung „Ophiuride von Kreis und Gerade“ setzt man den Kreis beispielsweise auf den Mittelpunkt , damit ist und sowie der Radius . Der Punkt wird mittels Kreisbogen und dem Radius bestimmt und anschließend die zur -Achse parallele Gerade gezogen. Die nächste Gerade verläuft durch und ; sie erzeugt dabei den Schnittpunkt . Abschließend wird die Strecke in halbiert. Der so erzeugte Punkt liegt auf der Ortslinie der Ophiuride.
- Wird der Punkt auf der Geraden bewegt, generiert Punkt den gesuchten Graphen der Ophiuride von Kreis und Gerade:
- [17]
Mittels Doppelgnomon
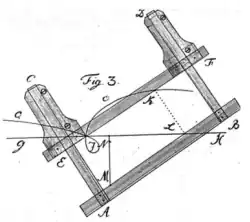
Das Gerät besteht aus zwei rechtwinkligen U-förmigen Holzgestellen. Die freien Schenkel des oberen verfügen in Längsrichtung über Aussparungen, in denen die freien Schenkel des unteren beweglich geführt werden. Auf dem Bügel des unteren ist ein Stift angebracht. Ihm genau gegenüber auf dem Bügel des oberen befindet sich ein Schreibstift .
Gegeben sei eine Gerade mit dem Teilpunkt . In sei eine Strecke der Länge abgetragen bis zum Punkt , auf dem Lot in eine Strecke der Länge bis zum Punkt . Das Gerät liegt dann mit seinem Innenbügel im Punkt fest an, gleichzeitig mit dem Außenbügel im Punkt . Der auf dem Außenbügel fixierte Punkt wird über den Stift in der „Rinne“ geführt. Dreht man den Bügel um den Punkt , so bewegt sich der Punkt auf voran. Der Schreibstift zeichnet dann die Kurve auf.[18]
Anwendungen
Würfelverdopplung
Die Kantenlänge des verdoppelten Einheitswürfels lässt sich mit der Ophiuride konstruieren als Quadratwurzel aus der Ordinate des Schnittpunkts . Setzt man und lässt (siehe Abschnitt Definition) die Werte von bis durchlaufen, so wird die Konstruktion von kubischen Wurzeln noch einfacher: Die Seite für die entsprechende Vervielfachung des Einheitswürfels ergibt sich jeweils direkt als Länge auf der Geraden zu .[19]
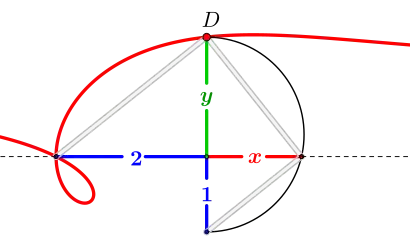
Ophiuride mit und generiert
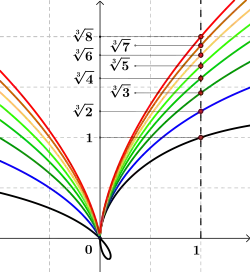
Vervielfachung des Einheitswürfels
Die Ophiuride als Trisektrix
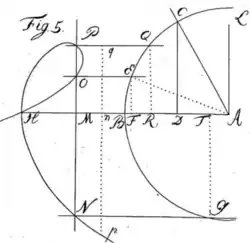
Uhlhorn, Dreiteilung des Winkels [20]
Abschließend stellt Uhlhorn eine Lösung des zweiten der Großen Probleme der Antike mithilfe der Ophiuride vor, der Dreiteilung eines Winkels (Bild 1).[21] Uhlhorn erklärt: Die zusätzlichen Lösungen zur Dreiteilung des –Winkels gelten für die Winkel und .[20]
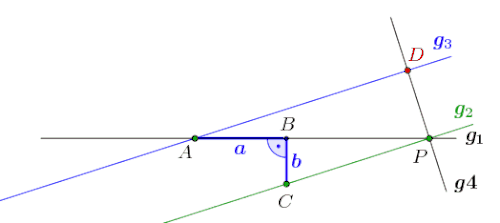
Konstruktion
(Bild 2, angepasst an Bild 1)
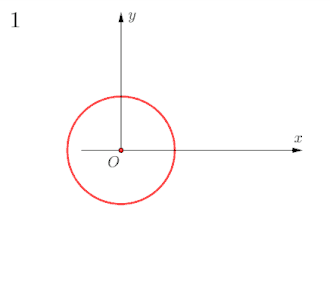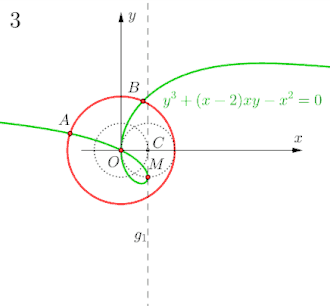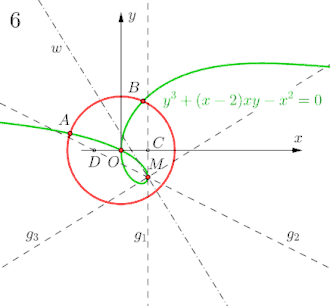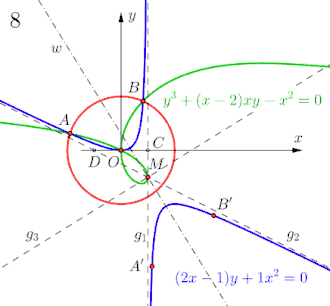
Auf einer Geraden wird zunächst der Punkt (entspricht dem Nullpunkt eines kartesischen Koordinatensystems) festgelegt und anschließend die Strecke bestimmt. Es folgen der Halbkreis mit Radius um , Schnittpunkt mit der Geraden ist (der zweite Schnittpunkt ist ohne Bezeichnung). Nun wird die Strecke in halbiert. Das Errichten der Senkrechten, auf in , schließt sich an. Der beispielsweise zu drittelnde Winkel wird mit dem Einzeichnen des Winkelschenkels eingetragen. Dabei ergibt sich auch dessen Supplementwinkel . Mit dem Fällen des Lots ab auf den feststehenden Winkelschenkel ergibt sich der Fußpunkt sowie mit der Sinuswert der Winkel und .
Weiter geht es mit dem Einzeichnen der Ophiuride mithilfe der Gleichung:
- .
Dabei schneidet die Ophiuride die Senkrechte über in den Punkten und . Abschließend zieht man eine Parallele zu durch und eine zweite Parallele durch . Die so erzeugten Schnittpunkte und mit dem Halbkreis liefern die gesuchten Winkel bzw. .
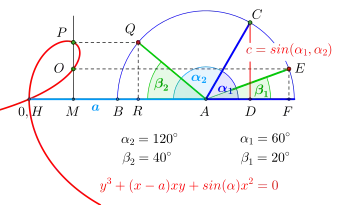
Winkeldreiteilung und Supplementwinkel
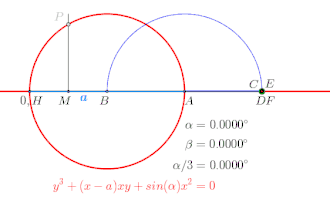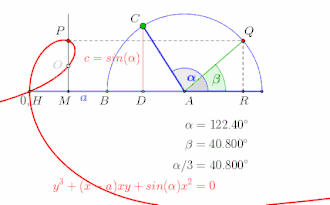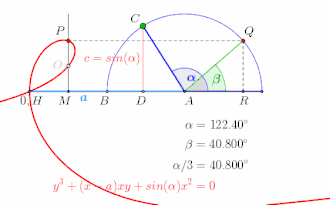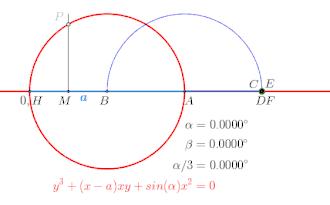
Winkeldreiteilung bis , Animation
Lösen kubischer Gleichungen
Die wichtigsten Stationen auf dem Weg zum exakten Lösen von kubischen Gleichungen markieren Omar Chayyam (um 1100) mit seinem Algebra-Buch,[22] François Vieta mit seiner Abhandlung „Supplementum Geometriae“ (1593) und René Descartes mit seiner „Géométrie“ (1637). Chayyam hatte für jede der 19 Typen kubischer Gleichungen eine Lösung „mit Kegelschnitten“ (Parabel und Hyperbel) vorgelegt. Vieta hatte grundsätzlich klargestellt: Mit der Neusis-Option sind alle Fälle abgedeckt. Eine Umsetzung in Form eines Beispiels fehlt bei ihm. I. Newton setzt diesen Ansatz später konkret um in seinen „Lucasian Lectures on Algebra“.
Descartes hatte gezeigt: Der Schnitt der Normalparabel mit einem Kreis reicht in jedem Fall aus.[23] Gleichzeitig hat Descartes die Möglichkeit eröffnet, für derartige Aufgabenstellungen neue Kurven einzuführen,[24] « […] qui peuvent aussi estres descrites par un mouvement regulier & continu […].[25] » Einfacher gesagt: Eine zulässige Kurve muss durch die stetige Bewegung eines Punktes erzeugbar sein. Seit dieser Zeit sind zur Festlegung von Punkten und Strecken einzig Kurven zulässig. Genau dies Cartesische Konzept greift Uhlhorn mit seinen Kurven auf. Die Lösungen, die sich speziell auf die Ophiuride gründen, zeichnen sich dabei dadurch aus – so betont Uhlhorn selbst –, dass man in jedem Fall „mit nur einer krummen Linie“ auskommt.[26]
Verallgemeinerung
Weitergehend zeigt Uhlhorn im Anschluss: Alle kubischen Gleichungen lassen sich mit der Ophiuride lösen.[26] Mit dieser grundlegenden Feststellung setzt Uhlhorn einen Schlusspunkt unter ein Jahrhunderte anhaltendes Bemühen um ein exaktes Lösen von höheren – insbesondere kubischen – Gleichungen. Die Zahlwerte der Lösungen von kubischen Gleichungen lassen sich in der Regel nur näherungsweise angeben. Im Beispiel liegt der sog. „casus irreducibilis“ der Cardanischen Formeln vor. Diese erfordern das Ziehen von kubischen Wurzeln aus imaginären Zahlen. Eine formal korrekte Einführung dazu – als Rechnen mit gerichteten Strecken – gelang dem Norweger Caspar Wessel (1799). Allgemein bekannt wurde dieser Ansatz erst durch eine Arbeit von Gauß (1831).[27]
Im folgenden Beispiel ergibt sich für den Hauptwert als Näherung Die geschlossene Darstellung lautet: .
Konstruktion
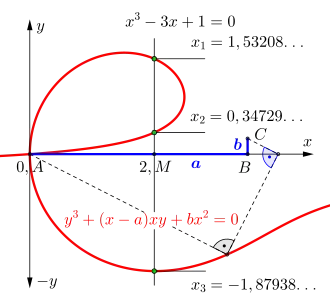
Graphische Lösung der kubischen Gleichung .
Es beginnt mit der Berechnung der Werte und , mit , für die Ophiuride.[28]
- , darin ist der Koeffizient von aus der kubischen Gleichung,
- ,
- , darin ist die Zahl aus der kubischen Gleichung,
- .
Es geht weiter mit dem Eintragen der Strecke ( entspricht dem Nullpunkt eines kartesischen Koordinatensystems) und der auf stehenden Senkrechten . Nun wird auf der Punkt mit Abstand bestimmt und in eine Senkrechte auf errichtet. Abschließend wird die Ophiuride anhand der folgenden Gleichung eingetragen:
- .
Die Ophiuride wird dabei dreimal von der Senkrechten auf durch geschnitten. Die Schnittpunkte und sind die drei möglichen Lösungen der gegebenen kubischen Gleichung.[29] Zwei davon sind irrational und eine entspricht :
- ,[30]
- ,
- ,
- .
Eine Hyperbel als Verwandte
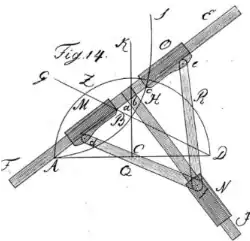
Eine Spiegelung am Einheitskreis führt für die Ophiuride zur Würfelverdoppelung auf eine Hyperbel.[31] Uhlhorn zeigt: Auf ebendiese Hyperbel führt der Ansatz der Neusis-Lösung von Sporus.[32] Vor allem aber lässt sich damit auch die Neusis-Lösung von Pappus retten. Immerhin hatte dieser erklärt, allein Kegelschnitte seien als Mittel zum Lösen zulässig. Eine Lösung, die sich an seine Vorgabe hält, hatte Pappus aber nie vorgelegt. Im Untertitel seiner „Entdeckungen“ heißt es bei Uhlhorn: „theoretisch und practisch abgehandelt“. So fehlt auch bei dieser speziellen Hyperbel nicht ein Werkzeug zu ihrer praktischen Erzeugung: Die Neusis-Bedingung der Längengleichheit der Abschnitte und wird hier rein mechanisch sichergestellt. Die Kurve wird aufgezeichnet durch einen Stift im Punkt .[33]
Konstruktion
Nach dem Einzeichnen des Einheitskreises (Inversionskreis) mit Radius um den Nullpunkt eines kartesischen Koordinatensystems, wird die Ophiuride mit den Parametern für die Würfelverdoppelung bzw. mithilfe der folgenden Gleichung eingetragen:
- .[34]
Die Ophiuride schneidet dabei den Inverskreis in den Punkten und sowie den Nullpunkt . Es folgt je ein Kreis mit Radius um sowie um den erzeugten Schnittpunkt . Die Gerade , senkrecht stehend zur -Achse und durch den Punkt verlaufend, schneidet die Ophiuride in .
Es folgt das Einzeichnen der Geraden durch und . Die Geraden und sind die Asymptoten der gesuchten Hyperbel. Nun wird der Winkel mithilfe der Winkelhalbierenden geteilt und die zu senkrecht stehende Gerade durch den Punkt gezogen. Um die gesuchte Hyperbel graphisch darstellen zu können, bedarf es bekanntlich außer den auf der Ophiuride liegenden drei Punkten und noch zwei weitere, also fünf auf der Hyperbel liegende Punkte.[35] Die beiden erforderlichen Punkte und erhält man durch Spiegelung der Punkte und an der Geraden .
Abschließend wird die Hyperbel mithilfe dieser fünf bestimmten Punkte eingezeichnet. Die Gleichung der Hyperbel ist bezüglich der irrationalen Koeffizienten noch zu vereinfachen, sodass gilt:
- .[36]
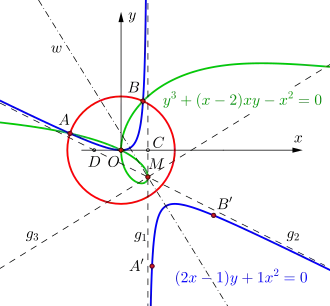
Animation mit 8 Bildern
Rezeptionsgeschichte
Uhlhorn weiß durchaus um die Zeichen seiner Zeit: Die Zukunft gilt einer Art von „Construction, wo die Gleichungen durch den Zug krummer Linien abgebildet werden.“[37] Die Ophiuride und ihre Bedeutung fallen in der Folgezeit bald dem Vergessen anheim. Die entscheidende Quelle für eine Rezeption der Uhlhornschen Kurven in der Fachliteratur ist das Werk von Loria (1902). Hier findet sich auch eine weitere der seiner Kurven, seine „Toxoide“ (Bogenlinie).[38] Die Zuschreibung dieser kubischen Duplikatrix zu Gohierte de Longchamp wird richtiggestellt.[38] Sie erweist sich als schlichtere, aber gleichmächtige Schwester der sog. „Kampyle des Eudoxus“.[39]
Literatur
- Thomas Little Heath: A History of Greek Mathematics. Volume 1. From Thales to Euclid. Clarendon Press 1921 (Nachdruck Elibron Classics 2006), S. 225–230 (archive.org).
- Wilbur Richard Knorr: The Ancient Tradition of Geometric Problems. Boston, 1986.
- S. Linden: Die Algebra des Omar Chayyam. Springer, Berlin / Heidelberg 2017, ISBN 978-3-662-55346-6.
- G. Loria: Spezielle algebraische und transzendente ebene Kurven. B. G. Teubner, Leipzig 1902 (quod.lib.umich.edu).
- Bodo von Pape: Die Großen Probleme der Antike II (Von Vieta bis Uhlhorn) Wuppertal 2022, ISBN 978-3-7568-3589-8 (Dissertation, bod.de).
- Diedrich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1, Oldenburg 1809.
Weblinks
- Ophiuride auf mathcurve
Einzelnachweise
- ↑ Heinrich Wilhelm Brandes: Lehrbuch der höhern Geometrie, in analytischer Darstellung. Kummer, Leipzig 1822, 176 ff., sowie Fig. 107 in Tab. V (uni-goettingen.de, Tab. V).
- ↑ Diederich Uhlhorn: Schlangenschwanzlinie. In: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 8 ff. (books.google.de).
- ↑ J. Chr. Sturm: Hin– und Wiederrukken … In: Des Unvergleichlichen Archimedis Kunst-Bücher. Nürnberg 1670, S. 105 (deutschestextarchiv.de).
- ↑ J.-E. Montucla: une sorte de tâtonnement. In: Histoire de Mathematique. Paris 1758, S. 177 (gallica.bnf.fr).
- ↑ Diederich Uhlhorn: § 23. Ohne Probieren … In: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 36 (books.google.de).
- ↑ Bodo v. Pape: Neusis-Lösungen in der Rezeption der Antike. (PDF; 219 kB) Technische Universität Dortmund, S. 1–4, abgerufen am 22. August 2025.
- ↑ Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 41–42 (books.google.de – § 32 „… auf drey verschiedene Arten erzeugen läßt.“, § 34 „… weil es sehr zuverlässig und sicher ist.“).
- ↑ Thomas Little Heath: The duplication of the cube. In: A history of Greek mathematics. Band 1. The Clarendon Press, Oxford 1921, S. 256–258 (englisch, Textarchiv – Internet Archive).
- ↑ W. R. Knorr: The Ancient Tradition of Geometric Problems. Dover Publicatons Inc., New York 1993, ISBN 0-486-67532-7, S. 59–60 (englisch).
- ↑ a b Bodo v. Pape: Die Großen Probleme der Antike. Von Eudoxus zu Uhlhorn II: Die Neuzeit. BoD – Books on Demand, Norderstedt 2022, S. 152.
- ↑ G. Loria: Spezielle algebraische und transzendente ebene Kurven. B. G. Teubner, Leipzig 1902, S. 49 (Fünftes Kapitel: Verallgemeinerung der Cissoide [PDF]).
- ↑ Bodo v. Pape: Die Großen Probleme der Antike. Von Eudoxus zu Uhlhorn II: Die Neuzeit. BoD – Books on Demand, Norderstedt 2022, S. 158–159. Aus der Grafik im Buch entnommen
- ↑ WolframAlpha: y³ + (x - a)xy + b (x - 1)² = 0
- ↑ Bodo von Pape: Die Großen Probleme der Antike. Von Eudoxus zu Uhlhorn II: Die Neuzeit. BoD – Books on Demand, Norderstedt 2022, S. 160–161.
- ↑ Bodo von Pape: Die Großen Probleme der Antike. Von Eudoxus zu Uhlhorn II: Die Neuzeit. BoD – Books on Demand, Norderstedt 2022, S. 160–161. Aus der Grafik im Buch entnommen
- ↑ WolframAlpha: x²(1 - y) - y³ = 0
- ↑ WolframAlpha: y³ + (x - 1,2)xy - 0,7x² = 0
- ↑ Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 31 (books.google.de): „Es ist leicht einzusehen, …“
- ↑ Bodo von Pape: Die Großen Probleme der Antike. Von Eudoxus zu Uhlhorn II: Die Neuzeit. BoD – Books on Demand, Norderstedt 2022, S. 150—151.
- ↑ a b Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, Tabelle I, Fig. 5 (images.sub.uni-goettingen.de).
- ↑ Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 51 (images.sub.uni-goettingen.de).
- ↑ Sebastian Linden: Die Algebra des Omar Chayyam. Springer, Berlin/Heidelberg 2017, ISBN 978-3-662-55346-6.
- ↑ Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 46, Descartes war erste… (books.google.de).
- ↑ Descartes: Discours de la Méthode & Essais. Hrsg.: Charles Adam & Paul Tannery. Band VI. Léopold Cerf, Imprimeur-Èditeur, Paris 1902, S. 434 (französisch, Textarchiv – Internet Archive).
- ↑ Descartes: Discours de la Méthode & Essais. Hrsg.: Charles Adam, Paul Tannery. Band VI. Léopold Cerf, Imprimeur-Èditeur, Paris 1902, S. 412 (französisch, Textarchiv – Internet Archive).
- ↑ a b Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 50 (books.google.de): „… kann man alle cubischen Gleichungen dadurch auflösen …“
- ↑ DMV: Eine kurze Geschichte der komplexen Zahlen
- ↑ Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 46 ff. (§ 41).
- ↑ WolframAlpha: y³ + (x - 3,5)xy + 1/4x² = x - 2 = 0
- ↑ WolframAlpha: x³ - 3x + 1 = 0
- ↑ Bodo von Pape: Die Großen Probleme der Antike. Von Eudoxus zu Uhlhorn II: Die Neuzeit. BoD – Books on Demand, Norderstedt 2022, S. 162.
- ↑ Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 8 ff. (books.google.de): „Auf diesem Wege lernte ich…“
- ↑ Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 45, „Es seyn (Fig. 14)…“ (books.google.de).
- ↑ WolframAlpha: y³ + (x - 2)xy - x² = 0
- ↑ Dörte Haftendorn: Kurven erkunden und verstehen. 7.6 Anwendungen der Kegelschnitte: „Kegelschnitt aus 5 Punkten“. Springer Spektrum, Wiesbaden 2017, ISBN 978-3-658-14748-8, S. 205.
- ↑ WolframAlpha: (2x - 1)y + x²
- ↑ Diederich Uhlhorn: Entdeckungen in der höhern Geometrie. Band 1. Oldenburg 1809, S. 46, Erster Abschnitt, Zweiter Absatz (books.google.de).
- ↑ a b G. Loria: Spezielle algebraische und transzendente ebene Kurven. B. G. Teubner, Leipzig 1902, S. 89 (Die kubische Duplikatrix und das parabolische Blatt [PDF]).
- ↑ Bodo von Pape: Die Großen Probleme der Antike. Von Eudoxus zu Uhlhorn II: Die Neuzeit. BoD – Books on Demand, Norderstedt 2022, S. 181–189.